Test Method for Bias and Scale Factor of Quartz Flexible Accelerometer: Comprehensive Guide and Temperature Sensitivity Analysis

"An in-depth analysis of the testing methods for the bias (zero bias) and scale factor of quartz flexible accelerometers is provided, including specialized techniques such as four-point rolling test and two-point test, as well as the calculation formula for temperature sensitivity. This is applicable to high-precision applications such as inertial navigation and spacecraft."

The bias (zero bias) and scale factor of quartz flexible accelerometers directly determine the measurement accuracy and long-term stability of the accelerometer, especially in high-precision application scenarios such as inertial navigation and attitude control. Therefore, they are two key performance indicators for evaluating quartz accelerometers.

The core significance of bias (zero bias) lies in its inherent system error of the accelerometer, which directly leads to the fundamental deviation of all measurement results. For example, if the zero bias is 1 mg, the measured value will add this error regardless of the actual acceleration. Zero bias will also drift with factors such as time, temperature, and vibration (zero bias stability). In inertial navigation systems, zero drift is continuously amplified through integration operations, resulting in cumulative errors in position and velocity. The temperature characteristics of quartz materials can also cause zero bias to change with temperature (zero bias temperature coefficient), so temperature compensation algorithms are needed to suppress this effect in high-precision applications. Scale factor refers to the proportional relationship between the output signal of an accelerometer and the actual input acceleration. The error in scale factor can directly lead to proportional distortion of the measurement results. The stability of scale factor directly affects system performance in high dynamic range or variable temperature environments. In the acceleration integration operation of inertial navigation, the scale factor error will be integrated twice, further amplifying the position error.

Therefore, the reason why bias and scale factor have become key performance indicators of quartz flexible accelerometers is that they are both fundamental error sources and key constraints on long-term stability. In system level applications, the performance of these two directly determines whether the accelerometer can meet the requirements of high precision and high reliability, especially in scenarios such as unmanned driving, spacecraft, submarine navigation, etc. where there is zero tolerance for errors

The bias test can be conducted through two methods: four point rolling test (0°，90°，180°，270°positions) or two-point test (90°，270°positions). The scale factor test can be conducted through three methods: four point rolling test (0°，90°，180°，270°positions), two-point test (90°，270°positions), and vibration test. Taking the four-point rolling test method as an example, this article explains how to obtain the bias and scale factor of an acceleration sensor.

1. Testing methods for bias and scaling factors:

a) Install the accelerometer on a specific test bench (multi tooth indexing head).

b) Start the test bench

c) Rotate the test bench clockwise to the 0°position, stabilize it, and record the output of multiple sets of tested products according to the specified sampling frequency. Take the arithmetic mean as the measurement result;

d) Rotate the test bench clockwise to the 90°position, stabilize it, and record the output of multiple sets of tested products according to the specified sampling frequency. Take the arithmetic mean as the measurement result;

e) Rotate the test bench clockwise to the 180°position, stabilize it, and record the output of multiple sets of tested products according to the specified sampling frequency. Take the arithmetic mean as the measurement result;

f) Rotate the test bench clockwise to the 270°position, stabilize it, and record the output of multiple sets of tested products according to the specified sampling frequency. Take the arithmetic mean as the measurement result;

g) Rotate the test bench clockwise to the 360°position, then counterclockwise to make the rotation angles at 270°, 180°, 90°, and 0°positions. After stabilization, record the output of multiple sets of tested products according to the specified sampling frequency, and take the arithmetic mean as the measurement result.

h) Calculate the bias and scaling factor of the tested product using the following formula (1) and (2).

K0 = 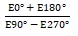   -------------------------------------- (1)

K1 =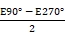   -------------------------------------- (2)

     Where:

        K0 -------Bias

        K1 -------Scale factor

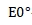        -------The total average of forward and reverse readings at 0°position

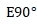        -----The total average reading of forward and reverse rotation at 90°position

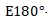        --- The total average reading of forward and reverse rotation at180° position

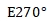        --- The total average of readings for forward and reverse rotation at 270°position

2. Test method for bias temperature sensitivity and scale factor temperature sensitivity

a) Start the test bench

b) Calculate the bias and scaling factors at each temperature point using the formulas (1) and formulas (2) at room temperature, the upper limit operating temperature specified by the accelerometer, and the lower limit temperature specified by the accelerometer.

c) Calculate the temperature sensitivity of the accelerometer using the following formula (3) and (4):

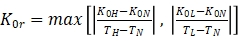     ---------------------(3)

where：

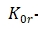---- Bias temperature sensitivity

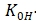----Bias of upper limit temperature of sensor

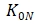----Bias of sensor room temperature

-----Bias of the lower limit temperature of the sensor

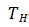------Upper limit temperature

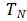------Room temperature

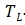-------Lower limit temperature

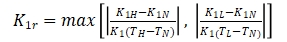     ---------------------(4)

Where:

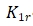----Scale factor temperature sensitivity

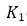------Scale factor

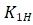----Scale factor for the upper limit temperature of the sensor

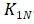----Scale factor of sensor room temperature

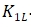-----Scale factor for the lower limit temperature of the sensor

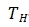------Upper limit temperature

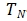------Room temperature

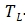-------Lower limit temperature

• Previous Post

  Testing Methods for Several Key Indicators of Fiber Optic Gyroscope | Zero Bias Stability, Scale Factor Nonlinearity & RWC Analysis

• Next Post

  Analysis of Mid-Low Precision FOG IMU Inertial Measurement System | Guide to Fiber Optic Gyro Navigation Scheme